Ce texte cherche à réinterroger la relation entre l’actuel et le virtuel de l’image à travers la figure topologique du ruban de Möbius – ou bande de Möbius –, surface compacte dont le bord est homéomorphe à un cercle. De fait, le ruban de Möbius ne possède qu’une seule face contrairement à un ruban classique qui en possède deux. À travers quelques exemples bien connus de films qui en utilisent le principe – qu’il s’agisse d’un jeu de formes abstraites comme dans la Symphonie Diagonale (1924) de Viking Eggeling ou de façon plus métaphorique, comme dans Lost Highway (1997) de David Lynch et Inception (2010) de Christopher Nolan, nous mettrons en place un relevé de ces formes rappelant le ruban de Möbius à l’image. En quoi les motifs géométriques qui apparaissent à la représentation ont-ils un impact sur la mise en scène ? De quels effets sont-ils responsables pour (re)penser certaines formes filmiques ? Pouvons-nous les penser comme des « formes filmantes » ? En interrogeant la virtualisation possible de l’actuel dans le défilé photogrammatique des images, on s’intéressera enfin au film S:TREAM:S:S:ECTION: S:ECTION:S:S:ECTIONED(1968-71) de Paul Sharits qui permettra de faire lien avec la mise en pensée de l’image par le spectateur. Devant la présence-absence d’un champ apparemment illimité, le ruban peut nous amener à réfléchir à certains dispositifs de réalité virtuelle (l’Oculus Rift). On passe alors des formes à l’image aux effets produits sur la vision.
Le ruban de Möbius : topologie d’une notion
Je commencerai par quelques évidences concernant cette figure topologique, qui, d’une certaine manière, dépasse le strict champ des mathématiques. Le ruban de Möbius1est bien cette déformation spatiale par transformations continues sans arrachages ni recollement des structures, ce qui, lorsqu’on parle de cinéma, pose déjà un problème ne serait-ce que par l’agencement des photogrammes dans un certain ordre au montage. Cependant, ce type de déformations permet de penser l’espace dimensionnel infini comme l’a montré la théorie des nœuds – l’étude mathématique de bouts de ficelles idéalisés – et notamment les travaux de Carl Friedrich Gauss2 liés à l’électromagnétisme (1831).
Premier questionnement : comment obtenir d’un point de vue pratique un ruban de Möbius ? En cousant par exemple bord à bord deux extrémités d’un ruban rectangulaire avec une torsion d’un demi-tour et en faisant tourner régulièrement un segment de longueur constante autour d’un cercle (ill. 1). C’est que le ruban ne possède qu’un seul bord et une seule face : si on suit du doigt le bord haut du ruban, on finira par revenir au niveau du point de départ, mais du côté bas. Et si l’on suit du doigt la face extérieure du ruban, on finira par revenir au point de départ, mais sur la face intérieure. Enfin, si l’on essaye de découper un ruban de Möbius en deux le long de l’axe médian, on obtient non pas deux rubans de Möbius, mais un seul ruban à deux faces. L’explication est assez simple : le fait de découper le ruban revient à lui ajouter artificiellement un bord. La surface que l’on obtiendra sera donc d’un seul tenant – le haut et le bas du ruban sont toujours dans un même prolongement – mais elle possédera deux bords distincts, retrouvant ici la forme du ruban classique. Par conséquent,le ruban de Möbius est un modèle qui crée une situation où il n’y a toujours qu’une seule voie. Une surface où les deux faces ne font qu’une puisque vous arrivez de l’autre côté sans jamais changer de face.

Ill. 1
Au-delà de ces quelques préalables, il nous faut pourtant aller plus loin dans l’exploration de cette figure.Dans une perspective plus philosophique,la figure du ruban de Möbius est circulaire : elle renvoie à une topologie générale de l’univers. A la question, comment les faces du ruban sont-elles pliées les unes sur les autres, le ruban met à jour une même angoisse entre les gens qui disent que le monde est plat – le monde de la chrétienté médiévale – ou ceux qui disent que le soleil tourne atour de la terre – le modèle géocentrique défendu par Aristote et Ptolémée. Sans toutefois répondre de l’aporie qu’engendre sa forme géométrique, l’observation des surfaces du ruban et son entrelacement permet de révéler le caractère sphérique de notre monde au lieu de son caractère topographique supposé plat. Nous pouvons également évoquer l’observation de la trajectoire des étoilesqui est un bon exemple afin de soutenir le caractère sphérique de notre monde : si les étoiles font des boucles, c’est parce que ce ne sont pas les étoiles qui tournent mais la terre qui tourne autour du soleil.
Le celluloïd tramé
Si je projette la problématique du ruban sur le film celluloïd, cela peut correspondre à la trame narrative qui se déroule – se déplie – et finit par revenir au même endroit : nous revenons au point de départ mais les choses sont inversés. Un personnage pourrait prendre la place d’un autre personnage. C’est d’ailleurs tout le principe scénaristique qui soutient les films de Lynch et notamment Lost Highway (1997) ou Mulholland Drive (2000). Dans une perspective formaliste, il est sans doute plus intéressant de penser le ruban comme un processus de renversement des formes lors de son passage du réel à l’écran : dans le monde réel, le ruban de Möbius est un espace bidimensionnel plié dans un espace tridimensionnel. Au cinéma, il devient la métaphore virtuelle du temps telle une « constellation de temporalités3 » fonctionnant sur le mode circulatoire d’un espace tridimensionnel sur une surface bidimensionnelle (l’écran plat de la projection). En guise de premier exemple, revenons sur La Symphonie Diagonale (1924), classique de l’avant-garde réalisé par Viking Eggeling. Le film est construit à partir de 6720 dessins : des colonnes stylisés en noir et blanc ou des formes géométriques en diagonales parcourent le cadre en ses bordures supposées de la droite vers la gauche (et inversement). L’alternance photogrammatique met à jour un tracé se construisant ou s’effaçant progressivement. Un jeu sur des formes courbes – deux demi-cercles de circonférences inégales – puis un retour sur des colonnes avec des sortes d’anses et de dessins complexes (le film part de la ligne et non de la surface) participent à l’idée d’une sorte de danse cosmique faite de formes abstraites (ill. 2 et 3). La métaphore du ruban de möbius s’épanouit ici dans un renversement rétrogradé de formes qui vont et viennent de façon répétées. Par conséquent, le rapport entre verticalité et horizontalité tend à produire un espace unilatéral.

Ill. 2 et 3
Autre exemple : en formalisant dans Inception (2010) son concept de « rêve partagé », Christopher Nolan a tenté de reprendre la figure du ruban de Möbius. Sa vision d’un Paris dont l’architectonique pliée à 90°– construit à partir d’écrans verts et d’incrustations d’images de synthèse – soutient le caractère sphérique du ruban faisant alors advenir d’autres figures géométriques tel que le triangle de Penrose (1950). Cette séquence voit Cobb (Leonardo DiCaprio) montrant à Ariane (Ellen Page) comment s’introduire dans les rêves d’une autre personne en construisant un univers clos au cours duquel un quartier de Paris est plié sur un autre (ill. 4). Toutefois, le ruban de Möbius convoque de façon sans doute trop littérale l’organisation des différents espace-temps convoqués à partir de l’infiltration du subconscient des cibles par un extracteur.

Ill. 4
L’actuel et le virtuel de l’image
Dans Lost Highway (1997), David Lynch met en place un réseau de figures dont les motifs mathématiques – cercles, spirales, cylindres – rappellent la sculpture géométrique du ruban de Möbius. La structure labyrinthique qui soutient les personnages en présence (la figure du double), trouve alors cohérence dans les formes visuelles usitées (cadrages obliques, décentrement de l’espace et autres déformations par le montage). Devant ce jeu formel, le héros est pris dans une boucle temporelle infernale où il ne peut s’échapper. Les derniers plans du film nous ramenant au début, emprisonnant le personnage dans un univers fait de pulsions destructrices. Le film est composé de deux parties (ou deux faces réversibles) : la première partie dans laquelle Fred Madison (Bill Pullman) est dans la réalité de sa vie de personne atteinte d’un trouble dissociatif de l’identité, jusqu’à sa condamnation pour le meurtre de sa femme et son internement en prison. La seconde partie dans laquelle Fred Madison vit un rêve de jeune homme garagiste mais où apparaissent en de multiples occasions des bribes de sa vie réelle et qui se conclut par l’assassinat de Renee Madison (Patricia Arquette). C’est pourtant moins le récit qui m’intéresse que le rôle de ces formes dans le milieu – réel ou imaginaire – où elles prennent place jusqu’à épouser certaines formes architecturales tout en courbures (ill. 5).

Ill . 5
Comment le film peut-il envisager la pliure dépliée d’une constellation de temporalités disparates que le ruban photogrammatique cherche à recomposer par juxtaposition ? Il y aurait donc à s’interroger sur le rapport entre l’actuel et le virtuel via le ruban de Möbius.Considérons pour commencer l’opposition facile et trompeuse entre réel et virtuel. Dans l’usage courant, le mot virtuel s’emploie souvent pour signifier la pure et simple absence d’existence, la « réalité » supposant une effectuation matérielle, une présence tangible. Le réel serait de l’ordre du « je le tiens » tandis que le virtuel serait de l’ordre du « tu l’auras », ou de l’illusion, ce qui permet généralement l’usage d’une ironie facile pour évoquer les diverses formes de virtualisation. Cette approche comporte une part de vérité mais elle est évidemment beaucoup trop simpliste pour fonder une théorie générale. Le mot « virtuel » vient du latin médiéval virtualis, lui-même issu de virtus, force, puissance. Dans la philosophie scolastique, est virtuel ce qui existe en puissance et non en acte. Le virtuel tend à s’actualiser, sans être passé cependant à la concrétisation effective ou formelle (par exemple, l’arbre est virtuellement présent dans la graine). En toute rigueur philosophique, le virtuel ne s’oppose pas au réel mais à l’actuel : virtualité et actualité sont seulement deux manières d’être différentes.
Il faut revenir ici à la distinction capitale entre possible et virtuel, que Gilles Deleuze a mise en lumière dans Différence et répétition (1968).Le possible est déjà tout constitué, mais il se tient dans les limbes. C’est un réel fantomatique, latent. Le possible est exactement comme le réel : il ne lui manque que l’existence. La réalisation d’un possible n’est pas une création, au sens plein de ce terme, car la création implique aussi la production innovante d’une idée oud’une forme. La différence entre possible et réel est donc purement logique.Le virtuel, quant à lui, ne s’oppose pas au réel mais à l’actuel. Contrairement au possible, statique et déjà constitué, le virtuel est le nœud de tendances ou de forces qui accompagne une situation, un événement, un objet ou n’importe quelle entité et qui appelle un processus de résolution : l’actualisation. Et c’est bien ce processus d’actualisation que tente de problématiser Lynch par l’image, qu’il s’agisse des éléments architecturés qu’il prélève au réel que la façon dont le montage construit une boucle temporelle.D’un côté, l’entité porte et produit ses virtualités : la deuxième partie du film lorsque le héros vit un rêve de jeune homme où apparaissent néanmoins des morceaux de sa vie réelle et où il est susceptible de recevoir des interprétations variées.D’un autre côté, le virtuel constitue l’entité : les virtualités inhérentes à un être, sa problématique, le nœud de tensions, de contraintes et de projets qui l’animent, les questions qui le meuvent sont une part essentielle de sa détermination. L’actualisation apparaît peut-être comme la solution d’un problème, une solution qui n’était pas contenue dans l’énoncé. Cette configuration dynamique de forces et de finalités peut passer par la figure du ruban de Möbius envisagé comme la métaphore soutenant la structure formelle du film. Il s’y passe autre chose que la dotation d’un choix possible parmi un ensemble prédéterminé. Une production de qualités nouvelles, un véritable devenir qui alimente le virtuel en retour. L’effet Möbius dans Lost Highway vient également du passage de l’intérieur à l’extérieur et de l’extérieur à l’intérieur. Cet effet se décline dans plusieurs registres : celui des rapports entre privé et public, pôle subjectif et objectif, carte et territoire. Les lieux et les temporalités se mélangent et s’interpénètrent : la ligne horizontale que forme cette route infinie dans la séquence d’ouverture finit par rejoindre les derniers plans du film, renvoyant au principe circulaire d’images repliées sur elles-mêmes (ill. 6).

Ill. 6
L’effet flicker du ruban de Möbius
S:TREAM de Paul Sharits (1971) est un film un peu à part dans sa filmographie. Comme le note Yann Beauvais : « Il ne s’agit pas ici d’un flicker film et, pourtant, le paradigme musical y est puissamment affirmé4 ». Cette structure filmique nous intéresse en ce qu’elle fonctionne sur le principe ambigu d’un vecteur d’orientation par écoulement du temps finalement impossible,renvoyant là encore à l’effet Möbius par renversement du motif de l’eau :l’aval et l’amont pris dans un présent perpétuel.La conception d’un assemblage chromatique et rythmique développé par le cinéaste rappelle en effet la partition de musique. Si cette comparaison demeure plus précise dans les films flicker, S:TREAM, qui fonctionne selon le principe du ruban refilmé, propose également la possibilité d’un contrepoint visuel. Quatre sources d’informations distinctes sont utilisées dans ce film : « des plans de rivière en surimpression (qui passent de six à aucun, en boucle trois fois), des rayures (huit blocs de trois rayures toutes les quatre minutes à partir de la quatrième), des mots répétés (au nombre de six, et qui se superposent les uns aux autres) et des bips et des collures (la relation entre les bips et les collures est modulaire)5 ». Comme toujours dans ses films, Sharits explore les mécanismes de perception et de projection. Il ajoute pourtant ici un élément de type matériel : le travail sur la pellicule. Il n’hésite pas à apposer la technique du grattage qui participe du flux d’images dans sa mise en mouvement. La physicalité de la pellicule, traitée comme une surface mouvante, permet d’interroger dans un sens quelque peu métaphorique, le fonctionnement du film comme le corps du film en tant que corps à la fois percevant et percevable. Sharits travaille d’ailleurs à la production d’une image cinématographique « qui n’est que par et dans la projection, une image avec laquelle on va induire de la pensée vers, sur le dispositif autant que sur les mécanismes qui nous permettent de saisir ce qui est jeu lors de la réception de ces propositions6 ». S:TREAM joue constamment sur les effets de surimpression dont les rayures discontinues et tremblantes rappellent le défilement de la projection cinématographique.
Enfin, la mise en surface de l’image fonctionne par contamination. Le travail de la surimpression à travers les motifs visuels (le flux des coulées d’eau, les marquages graphiques, les mots répétés qui se superposent) construit un espace étrange où chaque bloc de rayures nous oblige à appréhender le cadre autrement, lequel finit par disparaître, laissant au spectateur la prise de conscience de l’écran comme surface haptique. L’épaisseur des rayures cohabite et se confond avec les images incessantes de la rivière, renvoyant l’ensemble à un flux temporel continu. Les rayures amènent l’image à un écart constant entre ce qui semble être perçu comme la portion d’un espace réel et la façon dont les rayures déroutent la profondeur fictive de ce même espace. L’eau semble fusionner avec les rayures dans une forme globale d’encastrement qui fonctionne par compression (ill. 7). Le champ comme espace de représentation, de même que le cadre qui en révèle la surface matérielle, n’a plus lieu d’être. Plus le film avance, plus les espaces s’enchevêtrent et n’en finissent plus de rétracter l’ensemble à une forme d’atomisation visuelle.

Ill. 7
En destituant la valeur-limite du cadre, Sharits fait prendre conscience de l’écran comme élément intégrateur à notre espace de perception. Le corps du film s’exprime pleinement dans le caractère projectif de l’écran via la mise à jour du principe de défilement pelliculaire. Mais l’artiste n’en oublie pas de faire renter une donnée essentielle, qui permet d’asseoir la reconnaissance réciproque du rapport entre un corps qui voit (notre schéma corporel) et qui se projette dans cette forme temporelle qu’est le film. L’aspect temporel joue ici avec duplicité : à la forme temporelle du montage, Sharits superpose le motif du ruissellement de l’eau, venant par là affirmer une pensée de l’écoulement du temps qui rentre en contact manifeste avec notre corps percevant. Le film développe une structure temporelle étrange, où le spectateur est amené à s’interroger sur la perception même des objets et leur variation dans le temps. Le flot continu de l’eau et les rayures qui parsèment l’image imposent de s’en remettre continuellement à nos impressions visuelles. Quant à l’invariabilité des motifs, ils épousent les altérations imposées par le défilement7 comme autant de gestaltsà remettre en forme. Si le film déploie une pensée sur l’écoulement du temps à travers l’évocation du ruissellement de l’eau, cette succession de « maintenant » propose une métaphore confuse du temps exprimé à l’écran jusqu’à envahir l’espace habitable du spectateur. Comme le développe Merleau-Ponty dans la Phénoménologie de la perception (1945), la rivière qui s’écoule réactualise notre perception. Ce que je vois est présent et ce que je vois a un passé et un avenir : « Si le temps est semblable à une rivière, il coule du passé vers le présent et l’avenir8. » Mais le philosophe ajoute que pour l’observateur, l’avenir de ce flot est à la source (en aval) puisque l’eau qu’il observera plus tard est déjà passée : « Le temps suppose une vue sur le temps. Il n’est donc pas comme un ruisseau. Il n’est pas une substance fluctuante. Si cette métaphore a pu se conserver depuis Héraclite jusqu’à nos jours, c’est que nous mettons subrepticement dans le ruisseau un témoin de sa course9. » De la même manière dans le film de Sharits, les rayures à l’image fonctionnent comme des superpositions de motifs qui montrent « une tension entre le temps qui s’écoule et le temps arrêté10 » jusqu’à affirmer l’instabilité du cadre-écran qui va vers son implosion supposée.
Réalité virtuelle et liquidation du cadre
Comme son nom l’indique, la réalité virtuelle consiste à créer une nouvelle réalité – on retiendra à la suite des réflexions deleuziennes que le contraire de virtuel n’est pas la réalité mais bien cette notion d’actuel – grâce à des logiciels spécifiques élaborés par différents constructeurs11. La réalité virtuelle permet d’appréhender de nouvelles perspectives qui ne sont pas existantes dans le monde réel mais qui représentent un véritable monde immersif.Si cette réalité n’est pas (encore) palpable, elle n’en reste pas moins sensible, c’est-à-dire ressentie visuellement et de manière auditive sans compter la dimension haptique du dispositif. Comme je l’avais indiqué en introduction, nous allons établir un arrêt sur l’Oculus Rift périphérique informatique de réalité virtuelle conçu par l’entreprise Oculus VR, filiale de Facebook.L’appareil se présente sous la forme d’un masque recouvrant les yeux et attaché au visage par une sangle fermée à l’arrière du crâne. Un écran plat numérique est placé à quelques centimètres en face des yeux, perpendiculairement à l’axe du regard. Cet écran affiche une image stéréoscopique déformée numériquement pour inverser la distorsion optique créée par deux lentilles situées en face de chaque œil, dans le but d’augmenter le champ visuel et la définition en face de la fovéa.L’écran est placé sur le plan focal de ces lentilles, de telle sorte que l’image virtuelle ainsi créée se trouve projetée à l’infini. Divers capteurs permettent de détecter les mouvements de tête de l’utilisateur, ce qui permet d’adapter en temps réel l’image projetée sur l’écran, afin de produire l’illusion d’une immersion dans la scène restituée (ill. 8). La distorsion optique créée par deux lentilles situées en face de chaque œil, permet d’augmenter considérablement le champ visuel d’une image virtuelle qui semble se situer en un point infini, mais sans la réduction à distance du cadre pictural (qui ne fait que redoubler de façon contrôlée l’acte d’énonciation).Comment penser alors ce cadre-invisible ?Peut-on parler, alors qu’il s’agit d’un morcellement d’images recomposées virtuellement de liquidation du cadre ? Et que peut nous apporter la génération d’une image détaillée sur les 110 ° restitués par l’Oculus Rift,là où l’œil humain ne peut percevoir une image nette que sur une zone très réduite de son champ de vision (entre 3 et 5°)12 ? Certes, le dispositif comprend encore quelques lacunes quant à la connexion de notre propre regard en déplacement sur l’image – le rift est encore incapable de détecter l’ensemble des mouvements. Pour le moment, il n’y a pas d’alternative car les yeux de l’utilisateur peuvent se déplacer n’importe où sur l’image et le Rift est incapable de détecter ces mouvements. Mais si on associe le rift à un capteur de suivi des pupilles, il serait alors possible de déterminer l’orientation du regard et d’adapter l’image restituée en conséquence. Ces capteurs commencent à se développer. Ils sont de plus en plus petits et de plus en plus réactifs via la technique du rendu fovéal (calculer plusieurs fois l’image sur de multiples résolutions par un système de calques).
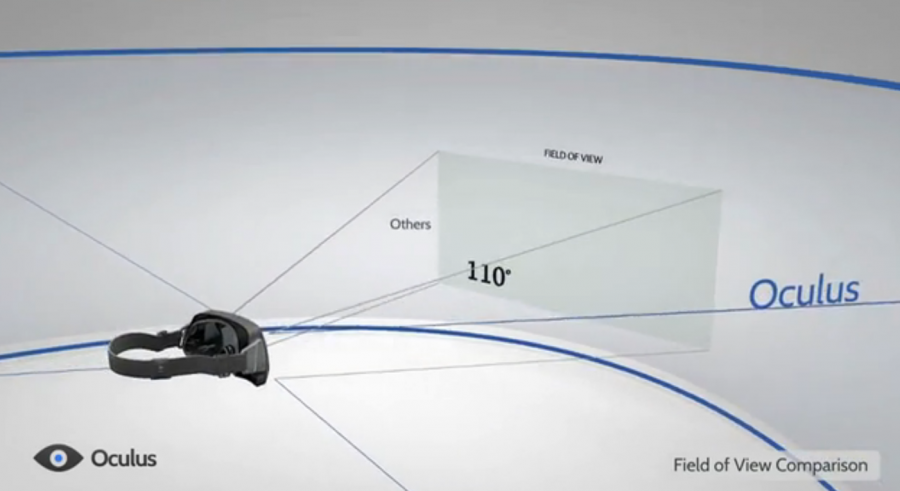
Ill. 8
Pour en revenir aux questionnements précédemment posés, comment définir l’expérience de l’espace que nous fait saisir ce médium sans cadre ? Avec son champ de vision supérieur à 100 degrés, l’Oculus Riftest le premier appareil de réalité virtuelle à permettre de recouvrir presque intégralement la vision humaine. Avec son assemblage de 14 à 24 caméras-capteurs – permettant de couvrir un espace allant jusqu’à 360° – l’apparence du monde réel fonctionne en vue stéréoscopique. Un paradoxe s’ouvre devant le fonctionnement du dispositif : si les images de l’Oculus Riftsont par essence hétérogènes, le spectateur fait face à une étonnante unicité qui vient renforcer l’impression de réalité. On cherche à se rapprocher des images jusqu’au vertige, voir à pénétrer dans l’image. Le casque de l’Oculus Rift et son pouvoir d’immersion – être transporté au cœur de l’événement – fait par ailleurs penser à d’autres types de projection comme la Polyvision ou le Cinérama. Devant ce champ visuel dont la ligne d’horizon semble illimitée, ne faudrait-il pas – tout en circonscrivant certaines limites au dispositif – établir un nouveau modèle de conscience dans le monde de la réalité virtuelle ? Dans un film en réalité virtuelle, le spectateur aurait la liberté de recomposer et de reconfigurer à sa guise le film selon l’endroit où il choisit de porter son regard. C’est d’autant plus plausible que l’ajout récent de périphériques permet au joueur de devenir non plus simple spectateur de l’action mais bien ce spectateur-acteur au pouvoir dynamique et qui n’est pas sans conséquences sur l’appréhension de l’environnement virtuel.
Le corps comme cadre naturel
Devant la présence-absence d’un champ apparemment illimité, il est sans doute vrai d’affirmer la possibilité pour un spectateur-acteur d’avoir la liberté de recomposer et de reconfigurer l’endroit où il choisit de porter son regard dans l’interface. De façon métaphorique, nous pouvons envisager la réalité virtuelle comme la forme filmique géométrique prenant les traits du ruban de Möbius.
En effet, l’agencement virtuel/actuel lié à un processus actif d’implication du corps dans le champ interactif, épouse les contours de cette forme ouverte à l’infini. La variabilité du point de vue motivé par le spectateur en tant que conscience, modifie systématiquement les rapports des objets et des êtres entre eux.Ce ruban est peut-être le modèle possible pour penser la réalité virtuelle. Dans la mesure où il figure une situation à deux faces qui n’en constitue pas moins qu’une seule voie, nous pouvons l’envisager comme un texte incomplet – comme troué – qui attend chaque spectateur potentiel.Cette ouverture s’accompagne d’une sensation proprioceptive importante à travers le sentiment d’un déplacement physique continu. Peut-on alors penser cette forme géométrique comme un agent actif dans l’espace de l’interface virtuelle ? Il ne tient qu’à nous d’en interroger les apports tout autant que les limites. Du cadre de l’image, on passe alors au corps humain comme cadre naturel : la réalité virtuelle jette le spectateur au milieu des images grâce à la position des capteurs qui en garantissent la continuité immersive. Ainsi, ces images ne peuvent plus être considérées come la copie d’un modèle préexistant, « une seconde chose », mais comme la création du modèle lui-même. Est-ce à dire que nous sommes, à l’image de ce que Mauro Carbone propose, face à des « écrans-prothèses13 » ? C’est-à-dire des images qui rétablissent – l’écran protège et cache – et proposent des possibilités corporelles.
Benjamin Léon
1 August Ferdinand Möbius est un mathématicien allemand principalement connu pour sa découverte du ruban de Möbius dont il en publia la construction en 1865. Cette figure topologique devient dès lors d’une grande importance en géométrie projective – application bijective continue – et tout ce qui concerne les notions intuitives de perspective et d’horizon.
2 La théorie des nœuds est une branche de la topologie qui étudie les bouts de ficelles.
3 L’expression provient d’un chapitre de Paris, capitale du XIXe siècle. Le livre des passages (1939) : « Il ne faut pas dire que le passé éclaire le présent ou que le présent éclaire le passé. Une image, au contraire, est ce en quoi l’Autrefois rencontre le Maintenant dans un éclair pour former une constellation. En d’autres termes, l’image est la dialectique à l’arrêt » (Walter Benjamin, Paris, capitale du XIXe siècle. Le livre des passages, traduit par Jean Lacoste, Le Cerf, coll. « Passage », Paris 1989, pp. 478-479).
4 Yann Beauvais, « Figment », in coll., Paul Sharits, Les Presses du réel, coll. « Monographies », Dijon 2008. p. 19.
5 Ibid.
6 Ibid., p. 22.
7 Nous citons à nouveau Yann Beauvais qui montre bien le principe de défilement inédit en jeu dans un film qui : « confronte le défilement du ruban au fil de l’eau, qui interroge les écarts entre l’enregistrement photographique créant l’illusion d’un espace tridimensionnel et l’espace physique bidimensionnel du ruban de pellicule » (op. cit., p. 19).
8 Maurice Merleau-Ponty, La Phénoménologie de la perception, Gallimard, coll. « Tel », Paris 2010, p. 472. En fait, et pour simplifier les propos du philosophe, il n’y aurait de passé et de présent que pour la conscience (sans quoi elle serait prise dans le présent), d’où l’idée d’une « succession de maintenant », sorte de présent éternel que le film remet en jeu par ce flot continu rendu à l’identique.
9 Ibid.
10 Rosalind Krauss, « Paul Sharits », Trafic, n° 29, P.O.L, Paris 1999, p. 91. Même si la tension évoquée par l’auteur renvoie davantage aux flickers films de Sharits où nous pouvons saisir le photogramme lorsqu’il survient à la projection.
11 La réalité virtuelle à destination du grand public a connu un essor important à partir de 2015 avec l’arrivée de casques et autres périphériques plus performants et abordables pour la grand public. On citera les périphériques Gear VR (Samsung), HTC Vive (HTC), Playstation VR (Sony) et l’Ouclus Rift (Facebook) dont nous rendons compte avec plus de précisions dans le texte.
12 Rappelons que le champ de la vision humaine est compris entre 120 et 180° (en vision binoculaire). De façon plus précise, chaque œil à un champ d’environ 150° (90 du côté temporal et 60 du côté nasal) ce qui permet d’avoir un champ de vision binoculaire de 120° avec deux champs monoculaires d’environ 40°.
13 Sur le concept « d’écrans-prothèses » voir le texte de Mauro Carbone « Le post-humain, la chair et le renversement du platonisme », Intervention au séminaire Le corps et le post-humain, 4 février 2011, http://www.maurocarbone.org/lyon/docs/text/Mauro_carbone_posthumain_chair_renversement_du_platonisme.pdf.
